Три эксперимента Liangzao
Fan,
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
С. Н. Пухов, ВлГУ, spuchov@mail.ru
В серии «Проблемы исследования Вселенной», Вып. 34.
Труды Конгресса-2010 «Фундаментальные проблемы естествознания и
техники», Часть III, стр.5-16. С-Пб.,
2010 опубликована статья Liangzao Fan. Three experiments
challenging Einstein’s relativistic mechanics and traditional
electromagnetic acceleration theory.
Первый эксперимент: Измерялась скорость электронов, ускоренных линейным ускорителем, чтобы выяснить, зависит ли эффективность ускорения линейного ускорителя от скорости электронов или нет. Второй эксперимент: Электроны с выхода линейного ускорителя, имеющие высокую скорость, бомбардировали свинцовую мишень, и измерялось увеличение температуры мишени. Третий эксперимент: Имеющие высокую скорость электроны с выхода линейного ускорителя инжектировались перпендикулярно в однородное магнитное поле, и измерялся радиус кругового движения электронов под действием отклоняющей силы Лоренца. Анализ всех трех экспериментов показывает: (1) Эффективность ускорителя уменьшается по мере увеличения скорости электронов и измеренная скорость электронов значительно меньше, чем рассчитанная по традиционной теории ускорения электромагнитным полем. (2) Результаты экспериментов не согласуются с формулами Эйнштейна для движущейся массы и кинетической энергии, но согласуются с формулами классической механики и Новой электродинамики движущихся тел. (3) Третий эксперимент подтверждает, что эффективность отклоняющей силы Лоренца также зависит от скорости отклоняемых электронов. §1. ВведениеВ соответствии с релятивистской механикой Эйнштейна, если объект с массой покоя m0 движется со скоростью V, тогда его движущаяся масса равна
а кинетическая энергия равна Ek = (m – m0)c2. Ученые проделали эксперименты с высокой скоростью, чтобы исследовать эти формулы Эйнштейна. Большинство экспериментов основывались на традиционной теории ускорения электромагнитным полем, которая рассматривает электромагнитную силу, действующую на движущиеся электроны, не зависящей от скорости электронов. Некоторые ученые в этом сомневаются. Чтобы проверить эти формулы Эйнштейна и традиционной теории ускорения электромагнитным полем, мы использовали высокоскоростные электроны, испускаемые из линейного ускорителя для осуществления трех видов экспериментов: [1][2] 1. Измерение скорости ускоренных электронов, чтобы вычислить кинетическую энергию, получаемую электронами, и сравнить её с энергией, затрачиваемой линейным ускорителем. 2. Бомбардировка высокоскоростными электронами свинцовой мишени и измерение увеличения температуры мишени вследствие кинетической энергии бомбардирующих электронов. 3. Инжектирование высокоскоростных электронов перпендикулярно в однородное магнитное поле и измерение радиуса кругового движения электронов под действием отклоняющей силы Лоренца.
Все три вида экспериментов были проведены на фемтосекундном линейном ускорителе в Шанхайском институте прикладной физики. Эксперименты предоставили четкие данные для проверки традиционной теории ускорения электромагнитным полем и формул движущейся массы и кинетической энергии. Анализируя данные этих трех экспериментов, в настоящей статье доказывается следующее: 1. Фактически действующая со стороны ускорителя сила, воздействующая на движущиеся электроны, зависит от скорости V электронов. Существует “явление c - V” (или “явление ветрового крыла”) так что чем больше скорость V электронов, тем меньше эффективность линейного ускорителя. Традиционная теория электромагнитного ускорения ошибочна. Бесконечное увеличение мощности ускорителя, включая сооружение дорогостоящего Европейского большого адронного коллайдера (БАК), есть бесполезная трата денег. 2. Эффективность отклоняющей силы Лоренца в однородном магнитном поле, которая действует на движущиеся электроны, зависит от скорости V электронов. Здесь также существует “явление c - V” которое необходимо учитывать. 3. Результаты всех трех экспериментов не согласуются с формулами Эйнштейна для движущейся массы и кинетической энергии, но согласуются с формулами классической механики и Новой электродинамики движущихся тел [3][4].
§2. Эксперимент по ускорению электронов в однородном электрическом поле§2.1. Методика и результаты экспериментаФронт электронов, испущенных из линейного ускорителя, продолжает свое прямолинейное и равномерное движение через прямую трубу длиной S = 1.43 м. Датчики были установлены на обоих концах секции трубы, чтобы измерить время влета t1и время вылета t2 электронного пучка в секцию и из секции. Скорость, полученная электронами благодаря линейному ускорителю, вычислялась по формуле V = S/(t2 – t1) Результаты эксперимента показаны в табл. 1:
Таблица 1
§2.2. Анализ
Из эйнштейновских формул 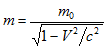
и Ek =( m – m0) c2 , имеем
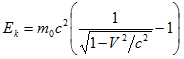
так что, измерив скорость V, мы можем вычислить кинетическую энергию Еk, полученную электронами, и эффективность линейного ускорителя Еk/E:
Таблица 2
Вызывает удивление, что кинетические энергии ускоряемых электронов оказываются большими, чем линейный ускоритель может им дать и эффективность линейного ускорителя оказывается большей, чем 100%!. Вероятно, что как релятивистская механика Эйнштейна, так и традиционная теория электромагнитного ускорения вызывают сомнение. В соответствии с Новой электродинамикой движущихся тел [3][4], которая базируется исключительно на галилеевском принципе относительности без постулата Эйнштейна о постоянстве скорости света и без постулата Лоренца о сокращении длины, если тело из неподвижного состояния ускоряется до скорости V , тогда оно приобретает кинетическую энергию Ek= mV2/2 . По этой формуле мы можем получить следующие результаты:
Таблица 3
По мере увеличения скорости электронов эффективность линейного ускорителя уменьшается. Это понятно, поскольку электромагнитная сила не может разогнать электроны до скорости света c , которая является скоростью передачи электромагнитных воздействий. Это похоже на случай между силой ветра и лодкой под парусами: скорость лодки под парусами никогда не может быть равна скорости ветра. Поскольку, если скорость лодки достигает скорости ветра, эффективная сила ветра, действующая на лодку с парусами, резко уменьшается. Большое количество силы ветра расходуется зря. В случае электромагнитного ускорения давайте называть это “явлениемс – V ”.
§3. Калориметрический эксперимент с электронами большой
скорости,
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Рабочая энергия линейного ускорителя, МэВ | 6 | 8 | 10 | 12 | 15 |
| Измеренное увеличение температуры [ °C] | 0,25 | 0,30 | 0,32 | 0,34 | 0,35 |
Температура мишени меняется очень незначительно, хотя уровни рабочей энергии линейного ускорителя изменяются в широких пределах.
§3.2. Анализ
Традиционная теория ускорения электромагнитным полем утверждает, что фактическая эффективная сила воздействия ускорителя на электрон не зависит от скорости электрона и вся рабочая энергия E ускорителя превращается в кинетическую энергию Ek, т. e., Ek = E. Если электроны действительно получили всю рабочую энергию линейного ускорителя, тогда путем использования формулы Эйнштейна
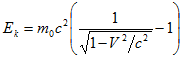
их скорости могут быть подсчитаны по формуле:
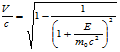 (3.1)
(3.1)
Кинетическая энергия Ek = E электронов вызывает увеличение температуры свинцовой мишени. Увеличение температуры может быть рассчитано по формуле:
Если Ek = E, то путем использования формулы Эйнштейна (3.1), расчетные значения увеличения температуры свинцовой мишени будут равны:
Таблица 5
| Рабочая энергия линейного ускорителя, МэВ | 6 | 8 | 10 | 12 | 15 |
| Расчетная скорость V электронов | 0.9969c | 0.9982c | 0.9988c | 0.9992c | 0.9995c |
| Расчетное увеличение температуры [ 0C] | 2.52 | 3.36 | 4.20 | 5.04 | 6.35 |
Расчетные значения увеличения температуры в таблице 5 значительно больше, чем соответствующие измеренные значения в таблице 4.
Более того, расчетные значения изменяются пропорционально рабочей энергии линейного ускорителя, тогда как измеренные значения изменяются очень мало. Это потому, с одной стороны, что когда скорость электронов достигает скорости света, их кинетическая энергия не увеличивается так резко, как рассчитано при использовании формулы Эйнштейна
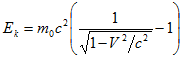
С другой стороны, эффективность линейного ускорителя резко уменьшается по мере того, как скорость электронов достигает скорости света (т. e., из-за “явления c −V ”, показанного в §2), так что электроны не достигали такой высокой скорости, которая рассчитана выше в таблице 5.
Давайте примем во внимание “явление c −V ”. Работа ускорителя состоит в том, чтобы заставить потенциальную энергию электромагнитного поля превратиться в кинетическую энергию электронов, т. e., превратить потенциальный напор линейного ускорителя в напор скорости электронов: Fdx = mυdυ .
В Новой электродинамике движущихся тел показано, что при движении заряда вдоль поля эффективная сила F может быть выражена
F=F0(1-V2/c2)
как, где v есть скорость электронов, а F0 есть номинальная сила воздействия ускорителя. С учетом всегда существующих при работе физических установок потерь энергии δE мы имеем
F=F0(1- δ - V2/c2)dx=mvdv
или
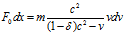
Номинальная работа, проделываемая ускорителем, потребляющим энергию E , равна ∫F0dx=E, которая ускоряет электрон от скорости = 0 до скорости = V :
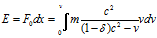 (3.2)
(3.2)
После интегрирования мы получаем:
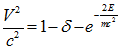 (3.3)
(3.3)
Используя (3.3) мы можем рассчитать фактическую скорость V электронов, ускоряемых определенной рабочей энергией E линейного ускорителя, а следовательно и их кинетическую энергию.
Известно[5], что в линейных ускорителях электроны очень быстро, при энергии 1-3МэВ, набирают скорость, близкую к скорости света. Степень приближения к скорости света определяется потерями энергии электронов в ускорителе и, как следует из эксперимента по отклонению электронов высокой энергии в однородном магнитном поле, составляет величину 0,997с.
С учетом того что на мишени выделяется полная энергия электронов мы можем также рассчитать увеличение температуры свинцовой мишени (Ek+mc2 ) х3,78/9.1 [°C, затраченную энергию линейного ускорителя ΔE=E –Ek и его эффективность E/ E k :
Таблица 6
| Рабочая энергия Eлинейного ускорителя, МэВ |
6 | 8 | 10 | 12 | 15 |
|
Рассчитанная скорость V электронов |
0.997 c | 0.997 c | 0.997 c | 0.997 c | 0.997 c |
|
Кинетическая энергия
Еk электронов, МэВ |
0,254 | 0,254 | 0,254 | 0,254 | 0,254 |
|
Расчетное увеличение температуры [ °C] |
0.32 | 0.32 | 0.32 | 0.32 | 0.32 |
|
Затраченная энергия линейного ускорителя ΔE, МэВ |
5,746 | 7,746 | 9,746 | 11,746 | 14,746 |
| Эффективность линейного ускорителя Еk/E |
4,23% | 3,2% | 2,54% | 2,12% | 1,69% |
Рассчитанные значения увеличения температуры свинцовой мишени в пределах погрешности совпадают с измеренными значениями из таблицы 4.
Очевидно, классическая механика вместе с учетом “явления c −V” могут объяснить, почему температура свинцовой мишени увеличивается так мало.
§4. Эксперимент по отклонению электронов высокой энергии в однородном магнитном поле
§4.1. Методика и результаты эксперимента
Поток электронов высокой скорости из линейного ускорителя инжектируется в камеру через прямолинейную корректирующую трубу толщиной 10 см, изготовленную из соединенных вместе свинца и железа, перпендикулярно однородному магнитному полю. Чтобы исключить любые внешние электромагнитные помехи, магнитное поле создается постоянным магнитом, а не электромагнитом. Зазор между двумя полюсами магнита имеет ширину в 2,5 [см], чтобы сделать магнитное поле между двумя полюсами как можно более однородным.
Три серии экспериментов были проделаны с тремя магнитами 0.121[Тесла], 0.081[Тесла] и 0.063[Тесла] соответственно.
Уровни рабочей энергии линейных ускорителей устанавливались равными 4МэВ, 6 МэВ, 9 МэВ, 12 МэВ, 16 МэВ и 20 МэВ. Примененная в эксперименте аппаратура показана ниже:

В таблице 7 внизу показаны измеренные значения радиусов круговых траекторий электронов, движущихся под действием отклоняющей силы Лоренца.
| Энергия линейного ускорителя E [ МэВ] | 4 | 6 | 9 | 12 | 16 | 20 | |
| 0,121[Тесла] | Измеренный радиус
R [см] |
~ 18 | ~ 18 | ~ 18 | ~ 18 | ~ 18 | ~ 18 |
| 0,081[Тесла] | Измеренный радиус
R [см] |
~ 27 | ~ 27 | ~ 27 | ~ 27 | ~ 27 | ~ 27 |
| 0,063[Тесла] | Измеренный радиус
R [см] |
~ 35 | ~ 35 | ~ 35 | ~ 35 | ~ 35 | ~ 35 |
Измеренные значения радиуса R для шести различных уровней энергии линейного ускорителя остаются почти постоянными.
Шесть небольших пятнышек размером с зерно кунжута, образованных слившимися вместе на экране следами электронов, образуют одно размером с зерно гороха пятно с шириной около 0,5[см], так, что имеются около R ≈17,75 [см], 26 ,75 [см], 34,75 [см] для случая самой низкой энергии в E = 4 [ МэВ] и около R ≈18,25 [см], 27,25 [см], 35,25 [см] для случая самой высокой энергии в E = 20 [ МэВ].
§4.2. Анализ
Традиционная теория считает, что сила Лоренца, которая отклоняет электрон движущийся в статическом однородном магнитном поле, не зависит от скорости V электрона. Если индукция статического однородного магнитного поля равна B , тогда теоретическая отклоняющая сила Лоренца равна F = eVB 0 . Отклоняющая сила Лоренца уравновешивается центробежной силой, действующей на электрон, движущийся по окружности вследствие отклонения. Поэтому кинематическое уравнение кругового движения электрона имеет вид:
mV2/R = eVB или R = mV/ eB , [4.1]
где m есть движущаяся масса электрона, а R есть радиус круговой траектории движения электрона.
Эйнштейновская формула
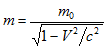
превращает уравнение (4.1) в уравнение:
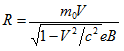
или
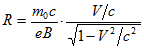 [4.2]
[4.2]
Традиционная теория ускорения в электромагнитном поле утверждает, что вся рабочая энергия E линейного ускорителя передается ускоряемому электрону и превращается в кинетическую энергию Ekэлектрона, так что Ek = E .
Как упомянуто выше в §3.2, традиционная теория ускорения в электромагнитном поле и эйнштейновская релятивистская механика вместе приводят к формуле (3.1). При использовании (3.1) мы можем рассчитать скорость V электрона и затем с использованием (4.2) мы можем рассчитать радиус R кругового движения электрона. Рассчитанные значения R показаны ниже:
Таблица 8
| E, МэВ | 4 | 6 | 9 | 12 | 16 | 20 | |
| V | 0.9919c | 0,9969c | 0,9986c | 0.9992 c | 0.9995 c | 0,9997c | |
| 0,121[tesla] | R, cm | 11.00 | 17,85 | 26,59 | 35,20 | 44,53 | 57,49 |
| 0,081[tesla] | R, cm | 16,43 | 26,66 | 39,72 | 52,58 | 66,52 | 85,88 |
| 0,063[tesla] | R, cm | 21,13 | 34,28 | 51,07 | 67,61 | 85,53 | 110,42 |
Рассчитанное значение R увеличивается почти пропорционально уровню E рабочей энергии линейного ускорителя, которое не соответствует результатам эксперимента. Таким образом, как традиционная электромагнитная теория ускорения, так и эйнштейновская релятивистская механика являются спорными.
Упомянутый выше калориметрический эксперимент с высокоскоростными электронами, бомбардирующими свинцовую мишень, выявил “явление c - V” (см. §3.2).
При использовании формулы (3.3), которая принимает в расчет “явление c - u”, мы можем вычислить скорость V электронов, влетающих в магнитное поле из линейного ускорителя. С другой стороны, в Новой электродинамике движущихся тел [3][4] показано, что при движении заряда в поперечном магнитном поле наблюдается зависимость взаимодействия заряда с полем от его скорости по закону:
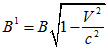
Учитывая это явление в (4,1) мы получаем совпадающую с (4.2) формулу:
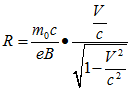 (4.3)
(4.3)
Как уже отмечалось, в линейных ускорителях электроны очень быстро, при энергии 1-3МэВ, набирают скорость, близкую к скорости света. Степень приближения к скорости света определяется потерями энергии электронов в ускорителе и, как видно из сопоставления таблиц 7 и 8, в данном случае скорость электронов была в пределах 0,997с.
С учетом этого по формуле (4.3) мы можем рассчитать радиус R :
Таблица 9
| E, МэВ | 4 | 6 | 9 | 12 | 16 | 20 | |
| V | 0,997c | 0,997c | 0,997c | 0,997c | 0,997c | 0,997c | |
| 0,121[tesla] | R, cm | 17,85 | 17,85 | 17,85 | 17,85 | 17,85 | 17,85 |
| 0,081[tesla] | R, cm | 26,66 | 26,66 | 26,66 | 26,66 | 26,66 | 26,66 |
| 0,063[tesla] | R, cm | 34,28 | 34,28 | 34,28 | 34,28 | 34,28 | 34,28 |
§5 Вопросы по Европейскому большому адронному коллайдеру (БАК)
Сообщалось, что самый мощный в мире Европейский БАК достиг ускорения протонов до уровня энергии в 3,5 [ТэВ] и протоны достигали скорости, равной
V ≈0,99999995c
Очевидно, что ученые ЦЕРН придерживались релятивистской механики Эйнштейна и традиционной теории ускорения электромагнитным полем при вычислении скорости своих протонов.
Действительно, согласно формуле (3.1), которая вытекает из релятивистской механики Эйнштейна и предполагает, что ускорение электромагнитным полем имеет 100% эффективность, если E = 3,5[ТэВ], тогда V ≈ 0,99999995c , что только на 15 м/c меньше, чем скорость света.
Ученые ЦЕРН верят, что при V ≈ 0,99999995c каждый протон имеет громадную движущуюся массу
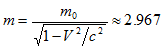 [ТэВ]
[ТэВ]
и кинетическую энергию Ek= 3,5[ТэВ].
Накопленная энергия двух сталкивающихся протонов равна 2Ek =7[ТэВ].
Скорость столкновения согласно закону сложения скоростей Эйнштейна равна
- 0,9999999999995c
Столкновение может привести к некоторым новым физическим открытиям главным образом вследствие огромной движущейся массы протона, движущегося с огромной энергией.
Однако согласно нашей формуле (3.3), которая основывается на классической механике и учитывает “явление c −υ ”, протоны были ускорены до меньших
скоростей. Более того, если даже протон двигается со скоростью С он обладает кинетической энергией, равной только 469,13 [МэВ], значительно меньшей, чем энергия БАК E = 3,5 [ТэВ].
Эффективность БАК поэтому составляет только около 0,013%
При увеличении V ускорение становится все менее и менее эффективным из-за “явления c −V ”.
Это происходит не вследствие того, что движущаяся масса частицы существенно увеличивается по мере того, как её скорость приближается к c согласно релятивистской механике Эйнштейна, так что ускорение становится все труднее и труднее.
Тем не менее, согласно галилеевскому закону сложения скоростей, скорость столкновения высока: V + V =( 2- δ) c ≈ 2с. Столкновение может привести к
некоторым новым физическим открытиям, главным образом вследствие огромных скоростей столкновения, а не вследствие больших движущейся массы протона и кинетической энергии, которые остаются малыми.
ЦЕРН собирается удвоить мощность своего БАК до 7 [ТэВ], чтобы ускорять протоны до скорости V = 0,999999991c (только приблизительно на 12,3 м/c выше, чем в случае, когдаэнергия БАК была равна Е = 3,5 [ТэВ] и только на 2,7 м/c меньше, чем скорость света.) так что Vsum~ C , m ≈ ∞и Ek ≈ ∞. Большинство ученых считают, что такие столкновения могут привести к Большому Взрыву, а также помогут им узнать сценарий Рождения Вселенной.
Однако согласно нашей формуле (3.3) энергия БАК, равная 7 [ТэВ] может ускорить протоны только до скорости.
Результаты почти те же самые, что и в случае энергии БАК, равной E = 3,5 [ТэВ]. Это происходит вследствие того, что “явление c −V” снижает эффективность БАК до значения 0.0065%.
Скорость столкновения равна
Какой бы большой мощностью ни обладал коллайдер, скорость столкновения всегда будет меньшей 2c.
Не обращая внимания на “явление c −V”, дорогостоящий БАК тратит огромное количество энергии и денег впустую для осуществления неэффективной деятельности.
Действительно, что ЦЕРН должен делать – это не удваивать мощность БАК, а увеличивать плотность тока для своего потока протонов. Потому что не всякие виды столкновений двух протонов могут вызвать новые физические явления. Столкновения по касательной не эффективны. Только точные лобовые столкновения, вероятность которых чрезвычайно мала, являются эффективными и чрезвычайно необходимы для открытия новых физических явлений.
И еще, при энергии БАК равной 7 [ТэВ], суммарная кинетическая энергия двух протонов при точном лобовом столкновении равна только 2Ek ≈ 938,26 [ МэВ].
Там не будет никакого Большого Взрыва или Рождения Вселенной.
§6. Заключение
1. Все три эксперимента доказывают, что традиционная теория ускорения электромагнитным полем и релятивистская механика Эйнштейна вводят нас в заблуждение.
Ускорение электромагнитным полем не может разогнать частицы до скорости V ≈ c .
И это не потому, что значительно увеличивается масса движения частицы по мере приближения к c , так что ускорение делается все труднее и труднее. Это происходит из-за “явленияc −V”, которое делает ускорение все менее и менее эффективным.
2. Релятивистская механика Эйнштейна не может объяснить результаты всех трех экспериментов, а классическая механика совместно с Новой электродинамикой движущихся тел может.
3. Отклоняющая сила Лоренца, которая обусловлена взаимодействием между статичным магнитным полем и движущимся магнитным полем движущегося электрона,
зависит от скорости движущегося электрона.
4. Чтобы исследовать “явление c −V ”, мы предлагаем физикам повторить эти эксперименты более точно и в более широком диапазоне скоростей.
Литература
1. Ji Hao, “Calorimetric Experiment to Test the Mass-Speed Relationship”, China Sci-Tech Achievements, 2009(1)
2. Ji Hao, “Experiment on the Motion of Electrons in a Homogeneous Magnetic Field”, China Sci-Tech Length and Breadth, 2009(6)
3. С.Н.Пухов, “Новая электродинамика движущихся тел “, Деп. в ВИНИТИ 9,06,1993г.,N1582-B93.
4. С.Н.Пухов, “Новая электродинамика движущихся тел “, Владимир, 1994г.
5. Е.Г.Комар, “Основы ускорительной техники“, с.349,М., Атомиздат, 1975г.
/Неизвестный
процессор/Охлаждение ПК/Электроника для ПК/Linux/Проекты, идеи/Полезные советы/Разное/
/Карта
сайта/Скачать/Ссылки/Обои/
При полном или частичном использовании материалов ссылка на "www.electrosad.ru" обязательна.
Ваши замечания, предложения, вопросы можно отправить автору
почтой.
Copyright © Sorokin A.D.©
![]()
2002 - 2020
